Question 1
Which of these fuels has the largest energy density?
- A) Wood
- B) Coal
- C) Sugar
- D) Vegetable oil
Answers and Explanations
Question 2
We have a setup as shown below. What does k, the spring constant of the spring have to be for the block to reach the height of 6 meters with a speed of 10 \(\text{ms}^{-1}\), if the block has a mass of 2 kg, and the spring is compressed by 10 cm? Assume the block starts from the bottom of the slope.
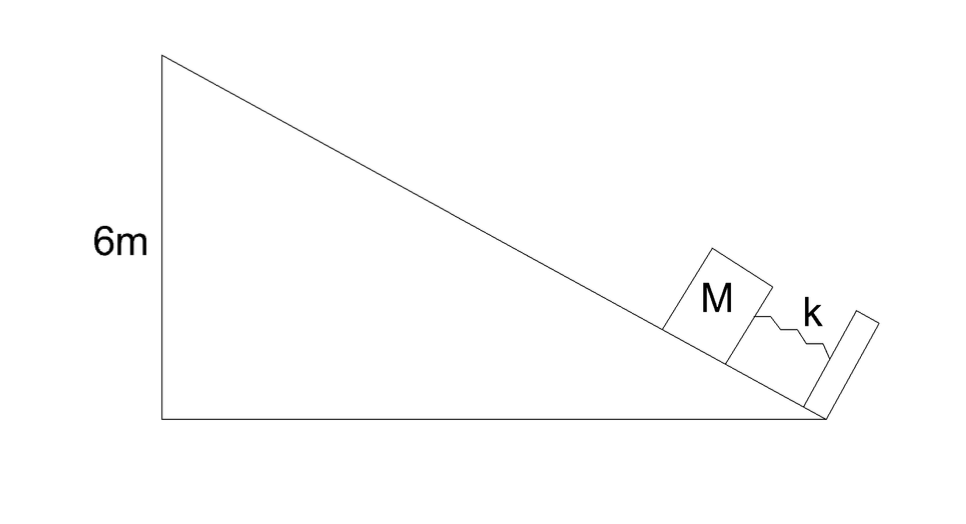
- A) \(25 \dfrac{kN}{m}\)
- B) \(44 \dfrac{kN}{m}\)
- C) \(20 \dfrac{kN}{m}\)
- D) \(2 \dfrac{kN}{m}\)
Question 3
We have a car of 1000 kg accelerating from 0 to 50\(ms^{2}\) over a distance of 200m. What is the power developed by the car?
- A) 5000 W
- B) 134560 W
- C) 120000 W
- D) 156250 W
Question 4
We supply an engine with 50W. Unfortunately, it only has an efficiency of 60%. What is the total power we can take out of the engine?
- A) 30W
- B) 83.3W
- C) This motor cannot supply power
- D) 50W
Question 5
We have a car of known mass M, and a graph showing its acceleration as a function of distance covered. How should the energy developed by the engine be calculated?
- A) The gradient of the graph
- B) The gradient of the graph multiplied by the mass M
- C) The area under the graph multiplied by the mass M
- D) We dont have enough information
Question 6
If we have a spring with spring constant k, and we compress with a distance x, the energy stored will be E. What will be the energy stored if we take a new spring with a spring constant 5k, and compress it by half the distance?
- A) \(\dfrac{5}{2} E\)
- B) \(\dfrac{5}{4} E\)
- C) \(\dfrac{2}{5} E\)
- D) \(\dfrac{4}{5} E\)
Question 7
\( 50 \, \text{kWh} \) is equal to:
- A) \( 1.8 \cdot 10^8 \, \text{J} \)
- B) \( 1.8 \cdot 10^6 \, \text{J} \)
- C) \( 0.9 \cdot 10^8 \, \text{J} \)
- D) \( 0.9 \cdot 10^6 \, \text{J} \)
Question 8
2 balls collide inelastically. Which of these is correct regarding the system's kinetic energy and linear momentum? (First column is momentum, second is kinetic energy)
- A) Not Conserved — Conserved
- B) Conserved — Conserved
- C) Not Conserved — Not Conserved
- D) Conserved — Not Conserved
Question 9
An object of mass \( m_1 \) has a kinetic energy \( E_1 \). A second object has double the mass and the same momentum as the first. What is the kinetic energy of the second object in terms of \( E_1 \)?
- A) \( E^2 \)
- B) \( \frac{E_1}{2} \)
- C) \( E \)
- D) \( 2E \)
Question 10
A frog of mass \( m \) jumps up vertically to a height of \( h \). The frog exerted the required energy for the jump in a time \( \Delta t \). What is the power developed by the frog?
- A) \( mgh\Delta t \)
- B) \( mh\Delta t \)
- C) \( mgh\Delta t^2 \)
- D) \( \frac{mgh}{\Delta t} \)
Question 11
A watermelon rests on a frictionless surface. A bullet is fired horizontally into the watermelon, and gets stuck inside. What happens to the system's total kinetic energy and momentum after the collision? (First column is kinetic energy, second column is momentum)
- A) Decreases — Unchanged
- B) Unchanged — Unchanged
- C) Decreases — Decreases
- D) Unchanged — Decreases
Question 12
Earth orbits the Sun in a circular orbit due to the gravitational force acting between the masses. What is the work done by this force in half of a period?
- A) \( \pi r F_G \)
- B) \( 2\pi r F_G \)
- C) \( F_G \cdot v_{\text{orbit}} \)
- D) 0
Question 13
A system containing a single spring has a load applied to it, and stores an energy of \( E_p \). A second, identical spring is then connected at the end of the first spring, and the same load is applied. What is the stored energy now?
- A) \( E_p \)
- B) \( 2E_p \)
- C) \( \frac{E_p}{2} \)
- D) \( \frac{E_p}{2} \)
Question 14
A pendulum undergoes SHM. Its kinetic energy is at a maximum in the equilibrium position. How many times during 1 period is the gravitational energy equal to the potential energy of the pendulum?
- A) 4
- B) 3
- C) 2
- D) 1