Detailed Answer

a) \((30x^3 + 2x)' = 3 * 30x^{3-1} + 2 = 90x^2 + 2\)

b) \((10x^4 + 6x^3 + 2x^2 + 10)' = 4*10x^{4-1} + 3*6x^{3-1} + 2*2x^{2-1} = 40x^3 + 18x^2 + 4x\)

c) \((\frac{1}{x^2} + 3)' = x^{-2} + 3 = -2x^{-3}\)

d) \((\frac{2x + 3x^2}{x})' = (2 + 3x)' = 3\)

e) \((\frac{x + x^2}{3x^3})' = (\frac{1}{3x^2} + \frac{1}{3x})' = -2 * 3x^{-2-1} + (-1) * 3x^{-1-1} = -6x^{-3} - 3x^{-2}\)

Detailed Answer

a)

\[ f'(x) = 9x^2 + 2x \]

b) To find the x-coordinates of the points where \( f'(x) = 0 \), we solve the equation \( 9x^2 + 2x = 0 \):

\[ 9x^2 + 2x = 0 \]

\[ x(9x + 2) = 0 \]

\[ x = 0 \quad \text{or} \quad 9x + 2 = 0 \]

\[ 9x = -2 \]

\[ x = -\frac{2}{9} \]

Therefore, the x-coordinates are \( x = 0 \) and \( x = -\frac{2}{9} \).

c) To find the gradient of the graph at \( x = 3 \), we substitute \( x = 3 \) into \( f'(x) \):

\[ f'(3) = 9(3)^2 + 2(3) \]

\[ f'(3) = 81 + 6 \]

\[ f'(3) = 87 \]

So, the gradient at \( x = 3 \) is 87.

d) To find the equation of the normal to \( f \) at the point (1, 2), we need to first find the gradient of the tangent at \( x = 1 \):

\[ f'(1) = 9(1)^2 + 2(1) \]

\[ f'(1) = 9 + 2 \]

\[ f'(1) = 11 \]

The gradient of the normal is the negative reciprocal of the gradient of the tangent:

\[ m_{\text{normal}} = -\frac{1}{11} \]

Using the point-slope form of the equation of a line \( y - y_1 = m(x - x_1) \), where \( (x_1, y_1) = (1, 2) \) and \( m = -\frac{1}{11} \), we get:

\[ y - 2 = -\frac{1}{11}(x - 1) \]

\[ y - 2 = -\frac{1}{11}x + \frac{1}{11} \]

\[ y = -\frac{1}{11}x + \frac{1}{11} + 2 \]

\[ y = -\frac{1}{11}x + \frac{23}{11} \]

So, the equation of the normal to \( f \) at the point \( (1, 2) \) is:

\[ y = -\frac{1}{11}x + \frac{23}{11} \]

Detailed Answer

a) To calculate it we first need to find the efficiency at year 2000, then the efficiency at year 2005. Therefore we have:

\[e(2000) = 10(2*2000^2 - 2000) = 79980000\]

\[e(2005) = 10(2*2005^2 - 2005) = 80380450\]

Then, we need to divide the difference in efficiencies by the difference in years, so:

\[\frac{80380450 - 79980000}{2005 - 2000} = 80090\]

b) To find it we first need to find the derivative and then plug into it our point of interest:

\[(10(2t^2 - t)' = (20t^2 - 10t)' = 40t - 10\]

Now, by plugging 2020 into this equation we get:

\[ 40 * 2020 - 10 = 80790 \]

Detailed Answer

a) \((\frac{1000000}{t})' = (1000000*t^{-1})' = -\frac{1000000}{t^2}\)

b) To find the time at which the house is decreasing by 10000$ per year we need to equalise this value to the derivative equation, so:

\[-\frac{1000000}{t^2} = -10000\]

\[-1000000 = -10000t^2\]

\[t^2 = 100\]

\[t = \pm \space 10\]

However, since naturally years cannot be negative, the only possible value is \( t=10 \).

c) The question starts similar to the previous part but with a different value:

\[-\frac{1000000}{t^2} \leq -5000\]

\[-1000000 = -5000t^2\]

\[t^2 = 200\]

\[t = \pm \space 14.142...\]

As it was in part (b), only positive years are possible. Also, in this case we are asked to find the first full year at which this decrease happens, so the first full year will be 15.

Detailed Answer

a) To get fixed costs we need to plug zero instead of \( x \), which will simply result in a value of 5000.

b) \((4x^3 - 3x^2 + 20x + 5000)' = 12x^2 - 6x + 20\)

c) To find the marginal cost at a specific point, we need to plug our point into the derivate equation. In this case it is:

\[12 * (1000)^2 - 6*1000 + 20 = 11994020\]

d) This part can be found by investigating the graph of the derivative, if it is positive, that means that at this point the function is incresing.

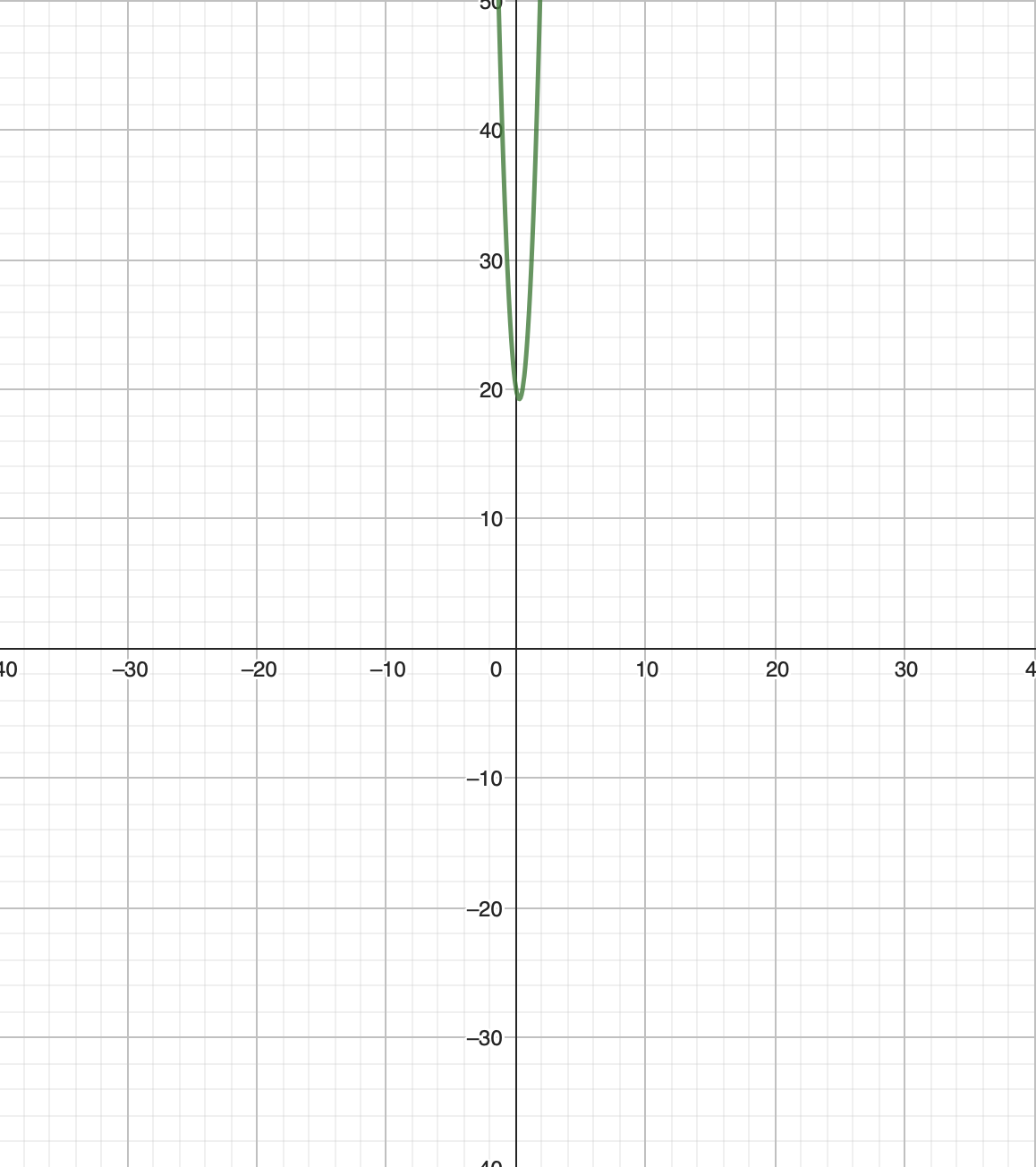
As it can be seen, the derivative does not cross the x-axis at any point, meaning that it is always positive, so the original function is always increasing.

Detailed Answer

a) To find the gradient of the function \( f(x) = 2x^5 + \frac{40}{3}x^3 \) at \( x = 1 \), we first compute the derivative \( f'(x) \).

\[ f'(x) = 10x^4 + 40x^2 \]

Substitute \( x = 1 \) into \( f'(x) \):

\[ f'(1) = 10(1)^4 + 40(1)^2 \]

\[ f'(1) = 50 \]

So, the gradient of the function at \( x = 1 \) is 50.

b) To find the x-coordinates where the normal to the function has a gradient of \( -\frac{1}{120} \), we first find the gradient of the tangent.

\[ m_{\text{tangent}} = -\frac{1}{-\frac{1}{120}} = 120 \]

We need to solve \( f'(x) = 120 \):

\[ 10x^4 + 40x^2 = 120 \]

\[ 10x^4 + 40x^2 - 120 = 0 \]

Let \( u = x^2 \). The equation becomes:

\[ 10u^2 + 40u - 120 = 0 \]

\[ u^2 + 4u - 12 = 0 \]

\[ (u+6)(u-2) = 0 \]

Since \( u = x^2 \) must be non-negative:

\[ x^2 = 2 \]

\[ x = \pm \sqrt{2} \]

So, the x-coordinates are \( x = \sqrt{2} \) and \( x = -\sqrt{2} \).

Detailed Answer

a) Knowing that the formula for the volume of a cylinder is equal to:

\[V = πr^2 * h\]

We can plug the known values into the formula:

\[3.5 = πr^2 * h\]

\[h = \frac{3.5}{πr^2}\]

b) In this case the formula for the area of a cylinder will be needed, since its outside needs to be painted:

\[A = 2πrh + 2πr^2\]

From that formula, the \(2πr^2\) part relates to the circular top and bottom. Since it is known that the cost for this part is 0.1 we have to multiply the two:

\[C_1 = 2πr^2 * 0.1 = 0.2πr^2\]

Now, the side is currently written in terms of r and h \((2πrh)\), and in the answer it can be clearly seen that only \( r \) can be used. Therefore, answer from part (a) needs to be used to change this equation:

\[2πrh = 2πr * \frac{3.5}{πr^2} = \frac{7}{r}\]

Now, it has to be multiplied by the cost of black paint, so 0.08:

\[C_2 = \frac{7}{r} * 0.08 = \frac{0.56}{r}\]

So the total cost is now:

\[C_{total} = \frac{0.56}{r} + 0.2πr^2\]

c) \((\frac{0.56}{r} + 0.2πr^2)' = -\frac{0.56}{r^2} + 0.4πr\)

d) We know that the radius is four times smaller than the height, so \( 4r = h \). So we can plug it into the equation for the volume:

\[h = \frac{3.5}{πr^2}\]

\[4r = \frac{3.5}{πr^2}\]

\[4r^3 = \frac{3.5}{π}\]

\[r^3 = \frac{3.5}{4π}\]

\[r = 0.653\]

Since there is no additional information, we round it to 3 significant figures.

e) Using the information for the lenght of radius from part (c) we can just plug it into the formula for total cost:

\[C_{total} = \frac{0.56}{r} + 0.2πr^2\]

\[C_{total} = \frac{0.56}{0.653...} + 0.2π(0.653...)^2\]

\[C_{total} = \frac{0.56}{0.653...} + 0.2π(0.653...)^2\]

\[C_{total} = 1.13$\]

Detailed Answer

a) First, we calculate the derivative:

\[ f'(x) = -\frac{4p}{x^5} + 1 \]

At \( x = -1 \), since it's a local maximum, we set \( f'(-1) = 0 \):

\[ f'(-1) = -\frac{4p}{(-1)^5} + 1 = -\frac{4p}{-1} + 1 = 4p + 1 \]

\[ 4p + 1 = 0 \]

\[ 4p = -1 \]

\[ p = -\frac{1}{4} \]

b) Let's substitute \( x = -1 \) and \( p = -\frac{1}{4} \) into the function:

\[ f(-1) = \frac{-\frac{1}{4}}{(-1)^4} + (-1) = -\frac{1}{4} - 1 \]

\[ f(-1) = -\frac{1}{4} - \frac{4}{4} = -\frac{5}{4} \]

The y-coordinate of the local maximum is \( -\frac{5}{4} \).

c) We have the derivative:

\[ f'(x) = -\frac{4p}{x^5} + 1 \]

Substitute \( p = -\frac{1}{4} \):

\[ f'(x) = -\frac{4 \left(-\frac{1}{4}\right)}{x^5} + 1 = \frac{1}{x^5} + 1 \]

Set \( f'(x) = 0 \):

\[ \frac{1}{x^5} + 1 = 0 \]

\[ \frac{1}{x^5} = -1 \]

\[ x = -1 \]

The root where \( f'(x) = 0 \) is \( x = -1 \).

d) This can be easily sketched in the GDC:

e) The function is increasing when its derivative is greater than zero. From the graph above we can see that the derivative is greater than zero for the interval \( (-\infty, -1) \) and for \( (0, +\infty) \), as there is a vertical asymptote at \( x=0 \).

Detailed Answer

a)

\[(x^2(2k - \frac{1}{4})x)' = 4kx - \frac{3}{4}x^2\]

b) To find the maximum value we have to equalise the derivative to 0, so:

\[4kx - \frac{3}{4}x^2 = 0\]

\[4kx = \frac{3}{4}x^2\]

\[4k = \frac{3}{4}x\]

\[x = \frac{16}{3}k\]

c) To solve this, both values need to be plugged into the profit function:

\[p(x) = x^2(2k - \frac{1}{4})x\]

\[10000 = 100^2(2k - \frac{1}{4}100)\]

\[1 = 2k - \frac{1}{4}100\]

\[2k = 26\]

\[k = 13\]

d) Now, the value obtained for \( k \) has to be plugged in into the \( x \) obtained in part (b), as it indicates the level of cakes maximizing the profits:

\[x = \frac{16}{3} * 13\]

\[x = 69.3\]

So the answer rounded to the nearest cake is 69.

e) To solve this question we need to go back to the original profit function and plug new information we have for \( k \):

\[p(x) = x^2(2k - \frac{1}{4})x\]

\[p(x) = x^2(2*13 - \frac{1}{4})x\]

Now, we have to equalise profits to zero to find the last point at which they don't lose money:

\[0 = x^2(2*13 - \frac{1}{4})x\]

By plugging this function into GDC we get the following:

So the answer is 104 cakes.

Detailed Answer

a) Given \( p = q + d \), we substitute into the expression \( 2p^2 + 5q^2 \):

\[ S = 2(q + d)^2 + 5q^2 \]

\[ S = 2(q^2 + 2qd + d^2) + 5q^2 = 2q^2 + 4qd + 2d^2 + 5q^2 = 7q^2 + 4qd + 2d^2 \]

To find the critical points, we take the first derivative and set it to zero:

\[ \frac{dS}{dq} = 14q + 4d \]

\[ 14q + 4d = 0 \]

\[ 14q = -4d \]

\[ q = -\frac{2d}{7} \]

Substituting \( q = -\frac{2d}{7} \) back into \( p = q + d \):

\[ p = -\frac{2d}{7} + d = \frac{5d}{7} \]

b) Now, we calculate the minimum value of the expression \( 2p^2 + 5q^2 \):

\[ S = 2\left(\frac{5d}{7}\right)^2 + 5\left(-\frac{2d}{7}\right)^2 \]

Let's separate each term:

\[ 2\left(\frac{5d}{7}\right)^2 = 2 \times \frac{25d^2}{49} = \frac{50d^2}{49} \]

\[ 5\left(-\frac{2d}{7}\right)^2 = 5 \times \frac{4d^2}{49} = \frac{20d^2}{49} \]

And add them together:

\[ S = \frac{50d^2}{49} + \frac{20d^2}{49} = \frac{70d^2}{49} = \frac{10d^2}{7} \]

Hence, we have shown that the minimum value of \( S \) is equal to \( \frac{10d^2}{7} \).

c) We take the second derivative of \( S \):

\[ \frac{d^2S}{dq^2} = 14 \]

Since \( \frac{d^2S}{dq^2} \) is positive, the function \( S \) has a minimum at \( q = -\frac{2d}{7} \).