Detailed Answer

1) The function is increasing as the x-coefficient is positive and we can clearly see that the y-intercept has to be at 20.

2) In this case after rearranging the equation we will be left with:

\(y = -\frac{1}{2}x + 5\)

That means that the function has to be decreasing and intercept the y-axis at the point 5.

3) If we multiply the two x-coefficients we get \(5 * (-0.2) = -1\). This means that these two functions have to be perpendicular.

4) \(0.2 * 0.25 ≠ -1\) and \(0.2 ≠ 0.25\). There is nothing special about these two gradients.

5) After plugging both A and B coefficients into each funciton we find that point B can only be on the third line.

6) We can read the y-intercept directly from this form of the equation.

7) We can put the equation in gradient-intercept form: \(y = \frac{-4x-8}{2} = -2x-4\). So the y-intercept is -4. Be careful not to simply take 8 in this case, as you can only do this in gradient-intercept form.

Detailed Answer

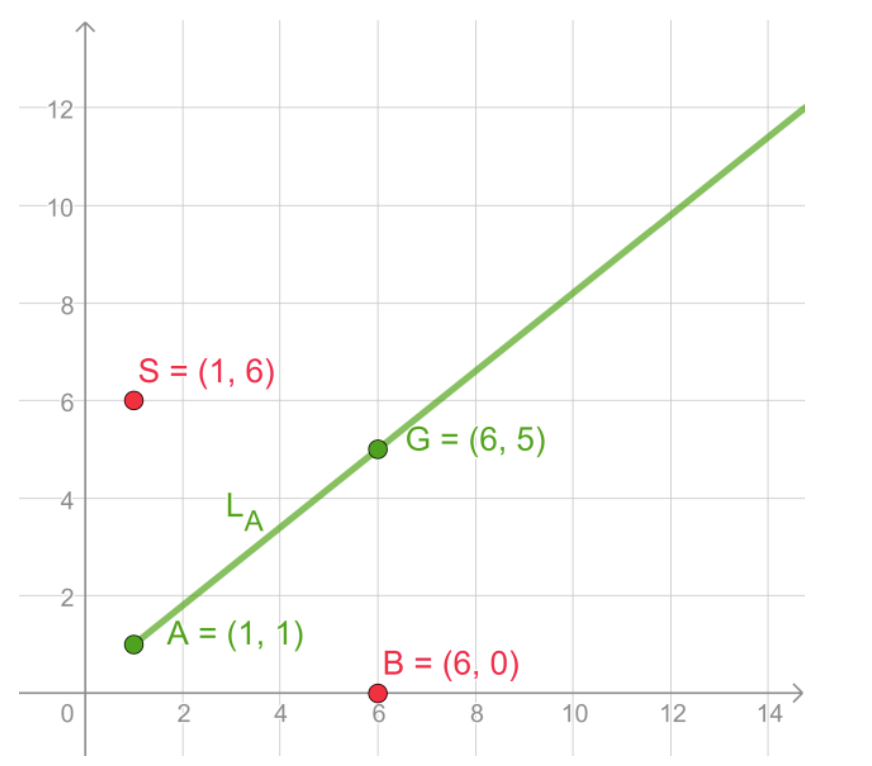
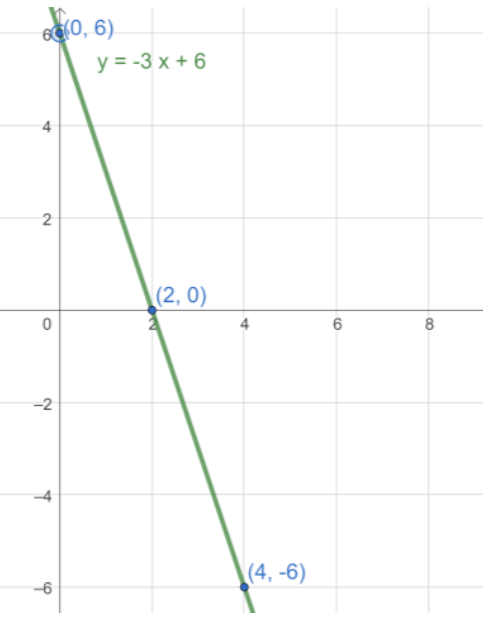
a) We calculate the gradient: \(\frac{y_2 - y_1}{x_2 - x_1} = \frac{-6 - 0}{4 - 2} = -3\). So the equation has the form \( y = -3x + c \). For the y-intercept, we replace \( x \) and \( y \) in the equation with the coordinates of one of the points: \( 0 = -3 \times 2 + c \), so \( c = 6 \).

b) By finding the unknowns in the previous point we pretty much already found the gradient-intercept form, which is \( y = -3x + 6 \).

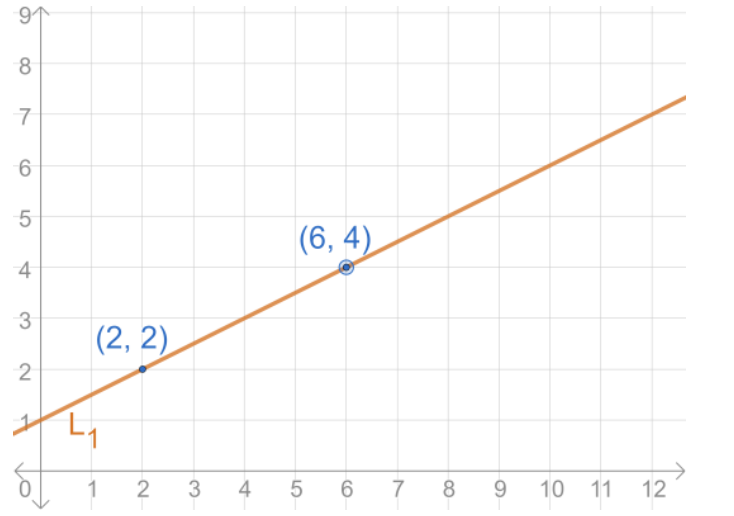
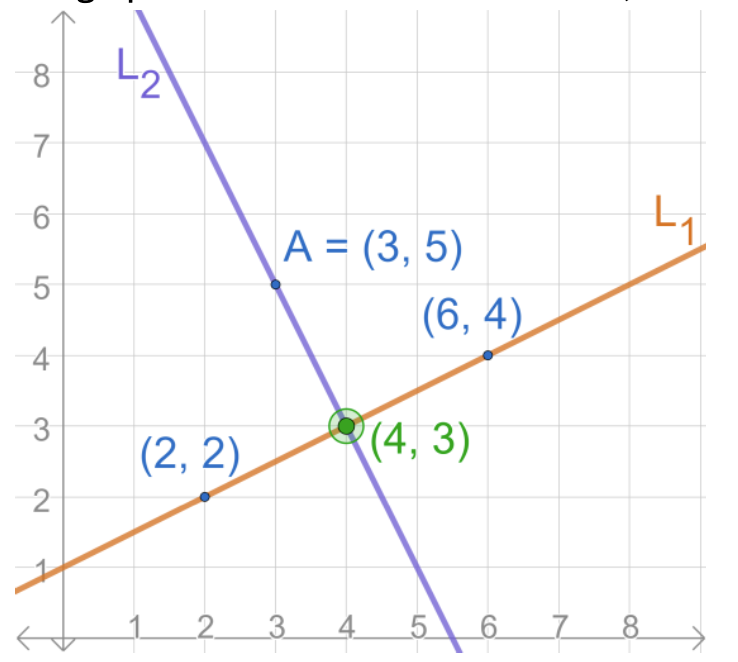
c) We can place the two points on a graph and draw the line that connects them. You can also place the y-intercept to help.

d) Parallel lines have the same gradient, so any equation with a gradient of -3 will work, like for example \( y = -3x \) or \( y = -3x + 3 \).

Detailed Answer

a) Find two points on the line with easily-read coordinates. For example, (2,2) and (6,4).

Then we calculate the gradient:

\[ m_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 2}{6 - 2} = 0.5 \]

The equation for \(L_1\) has the form \(y = 0.5x + c_1\)

We can read the y-intercept on the graph (coordinates (0,1)), or replace \(x\) and \(y\) in the equation with one set of coordinates. In this case, we can find: \(2 = 0.5 \times 2 + c_1\), so \(c_1 = 2 - 1 = 1\)

b) The gradient of \(L_2\) is such that \(m_1 \times m_2 = -1\) as they are perpendicular. This means that \(m_2 = -\frac{1}{0.5} = -2\). The equation for \(L_2\) has the form \(y = -2x + c_2\). If we replace \(x\) and \(y\) with the coordinates of \(A\), we get: \(-2 \times 3 + c_2 = 5 \implies c_2 = 11\)

c) We graph both lines on the calculator and find where they meet.

d) We can calculate it or find it by looking at a graph on the calculator. By calculating, we replace \(y\) with 0 in the equation for \(L_1\): \(0.5x + 1 = 0 \implies x = -2\)

e) We can use the same method as we did in part (d), so: \(-2x + 11 = 0 \implies x = 5.5\)

Detailed Answer

a) We can replace \(x\) by -2 in the equation and check if we get the right value for \(y\).

\[ 2.5 \times (-2) + 0.5 = -5 + 0.5 = -4.5 \]

−4.5 ≠ 4.2, so \(P\) isn’t on \(L\).

b) Using the same method. For \(A\) we have that:

\[ 2.5 \times (-1) + 0.5 = -2.5 + 0.5 = -2 \]

Which matches the coordinates of \(A\).

Then, for \(B\) we have that:

\[ 2.5 \times 3 + 0.5 = 7.5 + 0.5 = 8 \]

Which also matches.

c) \(M\)'s coordinates are:

\[ \left(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2}\right) = \left(\frac{-1 + 3}{2}, \frac{-2 + 8}{2}\right) = (1, 3) \]

d) First, we find the gradient \(m'\) of the bisector. It is perpendicular to \(L\), so the product of their gradients is -1, so:

\[ 2.5 \times m' = -1 \implies m' = -\frac{1}{2.5} = -0.4 \]

Then we use the coordinates of \(M\) to find \(c'\), because the bisector goes through the middle of the segment.

\[ -0.4 \times 1 + c' = 3 \]

\[ c' = 3 + 0.4 = 3.4 \]

So the equation for \(L'\) is \(y = -0.4x + 3.4\)

e) We replace \(x\) by \(x_P\) in the equation of \(L': -0.4 \times (-2) + 3.4 = 4.2\), which matches \(P\)'s coordinates.

f) \(P\) is on the bisector. Each point on a segment’s bisector is equidistant from the segment’s endpoints.

Detailed Answer

a) We find the intercepts immediately by reading the equations. We can also replace \(x\) by 0 to be sure.

b) We can graph the two lines on a calculator and find their intersection.

c) If \(L_3\) is perpendicular to the y-axis, then it is a horizontal line with an equation of the form \(y = c\). It goes through \(M\), so \(y = 2\), as \(y_M = 2\).

d) \(L_3\) is always equal to 2. It is parallel to the x-axis and never intersects it.

Detailed Answer

a) We draw a line through \(S\) and \(B\).

b) \(m_B = \frac{y_B - y_S}{x_B - x_S} = \frac{0 - 6}{6 - 1} = -\frac{6}{5} = -1.2\)

We use the coordinates of either \(S\) or \(B\). We choose \(B\) as it’s easy to replace \(y\) by 0, so: \( -1.2 \times 6 + c = 0 \implies c = 7.2\)

c) You can read it on your sketch, or graph both lines on a calculator, and find it out this way.

d) First, we find the gradient of the line that goes through \(S\) and \(G\): \(m_1 = \frac{5 - 6}{6 - 1} = \frac{-1}{5} = -0.2\)

The gradient \(m_2\) of the bisector is such that \(m_1 \times m_2 = -1\), so: \(m_2 = \frac{-1}{-0.2} = 5\)

The midpoint of \([SG]\) has coordinates \(\left(\frac{1 + 6}{2}, \frac{6 + 5}{2}\right) = \left(\frac{7}{2}, \frac{11}{2}\right) = (3.5, 5.5)\), and the bisector goes through it, so \(5 \times 3.5 + c = 5.5 \implies c = 5.5 - 17.5 = -12\)

The equation of the bisector is \(y = 5x - 12\).

e) All points on the bisector are equidistant from \(S\) and \(G\). This question can be reformulated as finding the intersection of \(L_C\) and the bisector.

This can be done by graphing both equations on the calculator or by completing your sketch.

Detailed Answer

a) You can place the y-intercept and any other point of your choice to get the following graph:

b) By adding the line \(x = 2\), we get the following:

c) Place the symmetry of two points on \(L_1\), and draw a line through them.

d) You can use the points you used to draw \(L_2\) to find the equation. For example, the symmetry of \((0, 2)\) is \((4, 4)\), and the symmetry of \((4, 0)\) is \((0, 0)\). This gives us the gradient \(\frac{4 - 0}{4 - 0} = 1\) and the intercept \((0, 0)\).

e) \([AB]\) and \([AC]\) are symmetrical, so they have the same length.

Detailed Answer

a) \(y=2(0)+5=5\)

b) \(0=2x+5\), so \(x=-\frac{5}{2}\)

c) 2

d) The product of the gradients must be -1. Hence it is \(-\frac{1}{2}\).

Detailed Answer

a) First we need to find the slope of \(L_1\). This is \(\frac{\Delta y}{\Delta x} = \frac{8-2}{-5-1}=-1\). Then we can plug into the point-slope form to find the equation of the line.

\[ (y-2)=-1(x-1) \\ y = -x +3 \]

b) First, we can find the midpoint.

\[ M = \left(\frac{1-5}{2},\frac{2+8}{2}\right) = \left(-2,5\right) \]

Then we remember that two lines are perpendicular if and only if the product of their slopes is -1. Since \(L_1\) has a slope of -1, \(L_2\) must have a slope of 1.

\[(y-5) = 1(x+2) \\ y= x+ 7 \]

Detailed Answer

a) \(17=5p+2\), so \(p=3\)

b) The gradient of \(L_2\) must be \(-\frac{1}{3}\) as \(3\cdot (-\frac{1}{3}) = -1\), which needs to be the case for perpendicular lines. Using point-slope form:

\[(y-17) = -\frac{1}{3}(x-5) \\ y = -\frac{1}{3}x + \frac{56}{3} \]

c) The equation in standard form is \(3y + x - 56 = 0\)

Detailed Answer

a) \(C : \left(\frac{2+4}{2},\frac{6+4}{2}\right) = \left(3,5\right)\)

b) \(-2(6)+5(2)+2=0\)

c) \(AC = \sqrt{(3-2)^2+(5-6)^2} = \sqrt{2}\)

d) First, we can find the gradient of \(L_1\), so we need to rearrange the equation. \(L_1: y=\frac{5}{2}x+1\). Since \(L_2\) will be perpendicular, their gradients' product must give \(-1\), hence the gradient of \(L_2\) is \(-\frac{2}{5}\).

e) We can use point-slope form: \[ (y-5)=-\frac{2}{5}(x-3) \\ y = -\frac{2}{5}x + \frac{31}{5} \]

f) This is a system of two equations: \[ y=\frac{5}{2}x+1 \\ y = -\frac{2}{5}x + \frac{31}{5} \] Solving this for \(x\) and \(y\) gives \(x=\frac{52}{29} \approx 1.79\) and \(y=\frac{159}{29} \approx 5.48\).