Detailed Answer

a) Let's first examine Electric Freaks. Since the usage is at 10kWh it means that the price will be $200 (it's below 20kWh). For Cheap Geeks on the other hand the cost has to be calculated by plugging the expected value into the function:

\[ z = 12 \times 10 + 500 = 620 \]

Thus, it can be clearly seen that Electric Freaks will be a cheaper option.

b) This can be easily calculated by taking the two values from the previous question: \( 620 - 200 = 420 \).

c) Now, since we are above the limit of 20kWh, the value has to be calculated by plugging the expected \( x \) value into the function:

\[ y = 21 \times 25 + 100 = 625 \]

d) First, the inverse of \( y \) has to be calculated, by inversing the order of \( x \) and \( y \):

\[ y = 21x + 100 \]

\[ x = 21y + 100 \]

\[ 21y = x - 100 \]

\[ y^{-1} = \frac{x - 100}{21} \]

\[ y^{-1}(155) = \frac{155 - 100}{21} = \frac{55}{21} \]

e) Since we know that at the level of 100kWh both functions are equal, the following two functions can be equalized:

\[ 12 \times 100 + 500 = 15 \times 100 + c \]

\[ c = 200 \]

Detailed Answer

a) To show it we simply need to plug the distance value into the function and show that the value is equal to 8:

\[ S = \frac{32}{2^2} = 8 \]

b) Again, it's all about plugging the value into the function:

\[ S = \frac{32}{8^2} = \frac{1}{2} \text{ dB} \]

c) This question, in simpler terms, asks us to find the inverse of the original function, which can be done by inversing the \( x \)'s with \( y \)'s and solving for the new \( y \):

\[ S = \frac{32}{d^2} \]

\[ S \times d^2 = 32 \]

\[ d = \sqrt{\frac{32}{S}} \]

Detailed Answer

a) The minimum RPM level to satisfy this function is 10, therefore:

\[ F = 16 \times (1.05)^{10} = 26.06 \]

b) We need to plug an RPM of 100 into the function:

\[ F = 16 \times (1.05)^{100} = 2104.02 \]

c) Firstly, the units of measurement need to be examined. Mark wants to get to a maximum of 20 liters and \( F \) is measured in \(\text{cm}^3\). Thus, liters need to be converted by multiplying the original value by 1000, leading to a value of 20000. Then, the \( r \) value needs to be obtained:

\[ 20000 = 16 \times (1.05)^{r} \]

\[ \frac{20000}{16} = (1.05)^{r} \]

\[ \ln\left(\frac{20000}{16}\right) = r \times \ln(1.05) \]

\[ r = \frac{\ln\left(\frac{20000}{16}\right)}{\ln(1.05)} = 146.15 \]

This can also be done directly in GDC.

d) To do that, two functions need to be directly compared:

\[ 50 + 2 \times (1.025)^r < 16 \times (1.05)^{r} \]

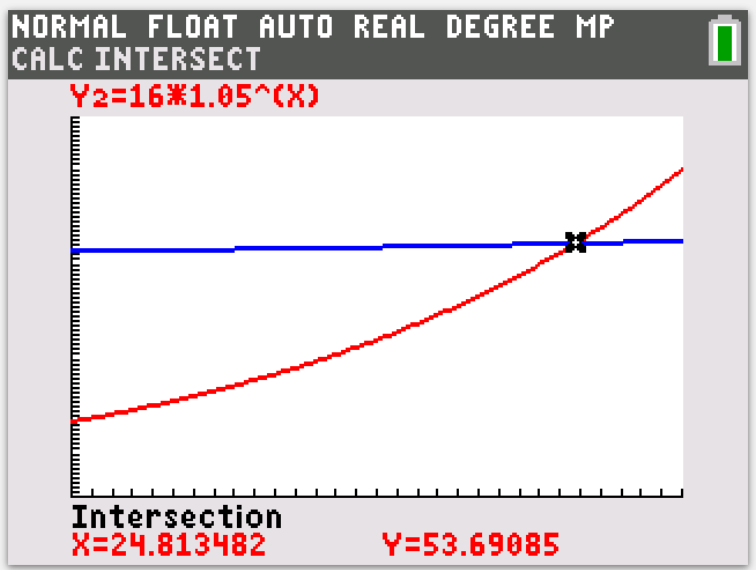
\[ r > 24.8 \]

Detailed Answer

a) The height of the wall can be found by finding \( x \) at its initial point, so when \( x = 0 \). By plugging \( x = 0 \) into both functions we get that \( z = 5 \).

b) To do that, we need to find the maximum points of both functions and then find their respective \( y \) values, which can be done with GDC.

The maximum of Scott's throw is when \( x \) is equal to \(\frac{3}{4}\). For that value, the height is equal to:

\[ H_s = 3 \times \left(\frac{3}{4}\right) - 2 \times \left(\frac{3}{4}\right)^2 + 5 = \frac{49}{8} \]

Similarly, the maximum for Miley's function is when \( x \) is equal to 2. For that value, the height is equal to:

\[ H_m = 5 + 4 \times (2) - (2)^2 = 9 \]

Therefore, we can clearly see that Miley threw the ball higher.

c) To answer this question, the \( x \)-intercept needs to be obtained for both functions. If the highest value for the \( x \)-intercept is greater than or equal to 10, then their mom will be hit by the ball. The \( x \)-intercepts can also be obtained by plugging the functions into the GDC.

For Scott, the \( x \)-intercept is equal to 2.5, and for Miley it is equal to 5. None of those values is greater than or equal to 10, meaning that their mom will not be hit by any of the balls.

Detailed Answer

a) To answer this question, we first need to write down the systems of linear equations we are dealing with by implementing the points provided in the question:

\[ t=1, h=25 \implies -x + y + z = 25 \]

\[ t=3, h=29 \implies -9x + 3y + z = 29 \]

\[ t=5, h=25 \implies -25x + 5y + z = 25 \]

Now, these can either be solved manually or, much more quickly, using a GDC. After plugging this set of three equations into GDC, we get the following solution:

\[ x = 1, y = 6, z = 20 \]

b) The ball hitting the ground is equivalent to the function crossing the h-axis, which happens when \( h = 0 \). Again, GDC can be used to answer this question, providing us with the answer of 8.39.

This is a quadratic function, meaning that it should have two roots; however, since the second root is negative (-2.39), this cannot be the answer, as time can't be negative.

c) This part is asking for the maximum of this function, which can also be easily found using a GDC. Thus, by plugging it into GDC, we find that the maximum is at point \( t = 3 \), for which the height is equal to 29.

Detailed Answer

a) To answer this, we simply need to input the value provided into the function:

\[ b = 5 \log(1.5 \times 20) = 7.39 \]

b) This question also requires us to input the information; however, we first need to find the function of time as a function of height:

\[ b = 5 \log(1.5t) \]

\[ \frac{b}{5} = \log(1.5t) \]

\[ 1.5t = 10^{\frac{b}{5}} \]

\[ t = \frac{10^{\frac{b}{5}}}{1.5} \]

At this point, we can plug in the value from the question, which is \( b = 20 \):

\[ t = \frac{10^{\frac{20}{5}}}{1.5} = 6666.67 \]

c) To answer this question, we first need to calculate the time taken for the tree to reach 8m, then calculate the time needed for it to reach double that amount, so 16m, and finally obtain the difference of the two time periods.

Thus, we can use the formula obtained in part (b) to calculate how long it took the tree to reach 8m:

\[ t = \frac{10^{\frac{8}{5}}}{1.5} = 26.54 \]

Then, we calculate how long it will take for the tree to reach 16m:

\[ t = \frac{10^{\frac{16}{5}}}{1.5} = 1056.60 \]

Therefore, the final answer is the difference between those two values, so 1030.06 days. Thus, it takes approximately 1031 full days for the tree size to double.

Detailed Answer

a) The starting fee is the constant term in the equation, so the moment at which the customer drives 0 kilometers, which is \(\text{5 USD}\).

b) The cost for a customer who traveled 12 km is calculated as: \(\text{C} = 5 + 1.5 \times 12 = \text{23 USD}\)

c) The graph of the function \(\text{C} = 5 + 1.5x\) for \(\text{0} \leq x \leq 10\) is a straight line starting at 5 USD and increasing linearly, as shown below:

d) We know that the payment of 18 USD was after the discount was applied, so the actual price that Mark was supposed to pay was:

\[ z \times 0.9 = 18 \]

\[ z = 20 \]

So, if he didn't have the discount he would have paid 20 USD. Now, for that price, the traveled distance is:

\[ 20 = 5 + 1.5x \]

\[ x = 10 \]

Thus, Mark traveled 10 km.

e) To find when RoadRunners is cheaper than Uber, set the costs equal: \(\text{5} + 1.5x < 1.75x\). Solving this inequality, we get \(\text{x} > 20 \text{ km}\).

Detailed Answer

a) The volume of the cylinder is given by: \[ V = \pi r^2 h \]. Since we know that \( x = 2r \), the final formula will be: \[ V = \pi \left( \frac{x}{2} \right)^2 h \]. Given that \( V = 80 \text{ cm}^3 \), we can solve for \( h \):

\[ 80 = \pi \left( \frac{x}{2} \right)^2 h \]

\[ 80 = \pi \times \frac{x^2}{4} \times h \]

Solving for \( h \):

\[ h = \frac{320}{\pi x^2} \]

b) The total surface area \( A \) is given by:

\[ A = 2 \pi r^2 + 2 \pi r h \]

\[ A = 2 \pi \left( \frac{x}{2} \right)^2 + \pi x h \]

Using \( h = \frac{320}{\pi x^2} \):

\[ A = \frac{1}{2} \pi x^2 + \frac{320}{x} \]

So, \( b = 320 \)

c)

d) The local minimum can be found directly in the GDC, and as we can see it happens at the point \( (4.67, 103) \).

Detailed Answer

a) The initial population of bacteria is given by the constant term in the function \( N(t) \). Therefore:

\[ N(0) = 25 \times (1.02)^0 = 25 \]

b) To find the amount of bacteria present after 1.3 hours (which is 78 minutes), we substitute \( t = 78 \) into the function:

\[ N(78) = 25 \times (1.02)^{78} = 117 \]

c) To find how much time it takes for the bacteria count to quadruple, first determine the time it takes for the bacteria to reach four times the initial population (which is 100 bacteria). Then find when the population reaches 1500. The difference between these times is the answer:

\[ 100 = 25 \times (1.02)^t \]

\[ \frac{100}{25} = (1.02)^t \]

\[ 4 = (1.02)^t \]

\[ \ln(4) = t \times \ln(1.02) \]

\[ t = \frac{\ln(4)}{\ln(1.02)} \approx 70 \text{ minutes} \]

Now, for 1500 bacteria:

\[ 1500 = 25 \times (1.02)^t \]

\[ \ln(60) = t \times \ln(1.02) \]

\[ t \approx 207 \text{ minutes} \]

The difference is around 137 minutes, which is 2.5 hours to the nearest half-hour.

d) (i) To find the number of bacteria per mL after 12 hours (720 minutes), use the growth function:

\[ N(720) = 25 \times (1.02)^{720} \approx 38910219.19 \text{ bacteria} \]

Now, divide by the volume of the flask:

\[ \frac{38910219.19}{250} \approx 155641 \text{ bacteria per mL} \]

d) (ii) Since the number of bacteria per mL (155641) is less than 2 million, the test is negative.

Detailed Answer

a) (i) To find the decay constant \( r \), we use the half-life formula. The decay constant \( r \) is related to the half-life \( T_{1/2} \) by the formula:

\[ r = \frac{\ln(2)}{T_{1/2}} \]

Given the half-life \( T_{1/2} = 5700 \) years:

\[ r = \frac{\ln(2)}{5700} \approx 0.000121 \text{ per year} \]

a) (ii) To find the amount of \( ^{14}\text{C} \) present 12500 years ago, use the formula \( C(t) = C_0 e^{-rt} \). Here, \( C_0 = 10 \, \mu\text{g} \) and \( t = 12.5 \) (in thousands of years):

\[ C(t) = 10 \times e^{0.000121 \times 12500} \approx 45.951 \, \mu\text{g} \]

b) (i) Given the normal ratio of \( ^{14}\text{C} \) to \( ^{12}\text{C} \) is \( 1.3 \times 10^{-12} \) and the sample contains 25 kg of \( ^{12}\text{C} \), we first convert the mass to grams:

\[ 25 \text{ kg} = 25 \times 1000 = 25000 \text{ g} \]

Then find the current ratio of \( ^{14}\text{C} \) using:

\[ \text{Current Ratio} = \frac{10 \, \mu\text{g}}{25000 \text{ g}} = 4 \times 10^{-6} \text{ (which is significantly different from the normal ratio)} \]

b) (ii) To estimate how long ago the sample dates back, use the ratio \( 1.3 \times 10^{-12} \) for \( ^{14}\text{C} \) to \( ^{12}\text{C} \) and the current ratio:

\[ \text{Current Ratio} = \frac{1.3 \times 10^{-12}}{1.4 \times 10^{-12}} \approx 0.4 \times 10^{-12} \]

The time elapsed \( t \) can be found using:

\[ \frac{\ln \left(\frac{1.3 \times 10^{-12}}{0.4 \times 10^{-12}}\right)}{0.000121} \approx 9.66 \text{ thousand years} \]

Detailed Answer

a) To find \( I_{D} \) for \( T = 300^{\circ} \text{K} \), substitute \( T \) into the given equation:

\[ I_{D} = 3.2 \times e^{\frac{6248}{300} - 21} \approx 2.69\]

b) To find an expression for \( T \) in terms of \( I_{D} \), rearrange the given formula:

\[ I_{D} = 3.2 \times e^{\frac{6248}{T} - 21} \]

\[ \frac{I_{D}}{3.2} = e^{\frac{6248}{T} - 21} \]

\[ \ln \left( \frac{I_{D}}{3.2} \right) = \frac{6248}{T} - 21 \]

Rearrange to solve for \( T \):

\[ T = \frac{6248}{\ln \left( \frac{I_{D}}{3.2} \right) + 21} \]

c) First, find the temperatures corresponding to each current:

\[ T_1 = \frac{6248}{\ln \left( \frac{7}{3.2} \right) + 21} \]

\[ T_2 = \frac{6248}{\ln \left( \frac{4}{3.2} \right) + 21} \]

Calculate \( \Delta T \):

\[ \Delta T = T_2 - T_1 \approx 7.56^{\circ} \text{K} \]

d) A 12% drop in temperature means the new temperature \( T_{\text{new}} \) is:

\[ T_{\text{new}} = 0.88 \times T \]

The ratio of the currents is:

\[ \frac{I_{\text{new}}}{I} = \frac{e^{\frac{6248}{0.88T} - 21}}{e^{\frac{6248}{T} - 21}} = e^{\frac{6248}{0.88T} - \frac{6248}{T}} \]

Simplify this ratio:

\[ \frac{I_{\text{new}}}{I} = e^{\frac{6248 \times (1 - \frac{1}{0.88})}{T}} = e^{\frac{852}{T}} \]

e) When \( T = 300 \text{K} \), substitute \( T \) into the ratio expression:

\[ \frac{I_{\text{new}}}{I} = e^{\frac{852}{300}} \approx 17.12 \]