Question 1No Calculator
[Maximum mark: 6]
Consider an arithmetic sequence in which \( u_5 = 18 \) and \( u_9 = 30 \).
a) Find \( d \)
b) Find \( u_1 \)
c) Find \( u_n \)
Question 2Calculator
[Maximum mark: 7]
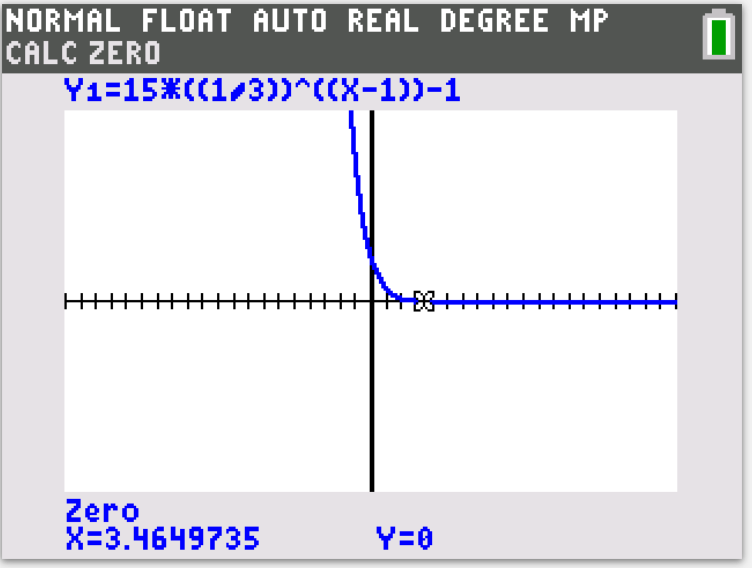
Consider a geometric sequence in which \( u_1 = 15 \) and \(r = \frac{1}{3}\)
a) Find \( u_5 \)
b) Which will be the first term with its value below 1?
c) Find \( S_7 \)
Question 3Calculator
[Maximum mark: 5]
Consider a sequence: \(80, 20, 5, \frac{5}{4}...\)
a) Is this sequence geometric? If yes, why? If not, what type of a sequence is it?
b) Hence, find \( S_{10} \). Round your answer to two decimal points.
Answers and Explanations
Show Answer
a) Yes, the common ratios are the same
b) 106.67
Question 4
Calculator
[Maximum mark: 5]
On the first day of March 2023, Alex planted 12 flowers in his garden. The number of flowers he plants on each subsequent day of the month forms an arithmetic sequence. The number of flowers he is going to plant on the last day of March is 72.
a) Find the common difference of this arithmetic sequence.
b) Calculate the total number of flowers Alex is going to plant during March.
Question 5
Calculator
[Maximum mark: 8]
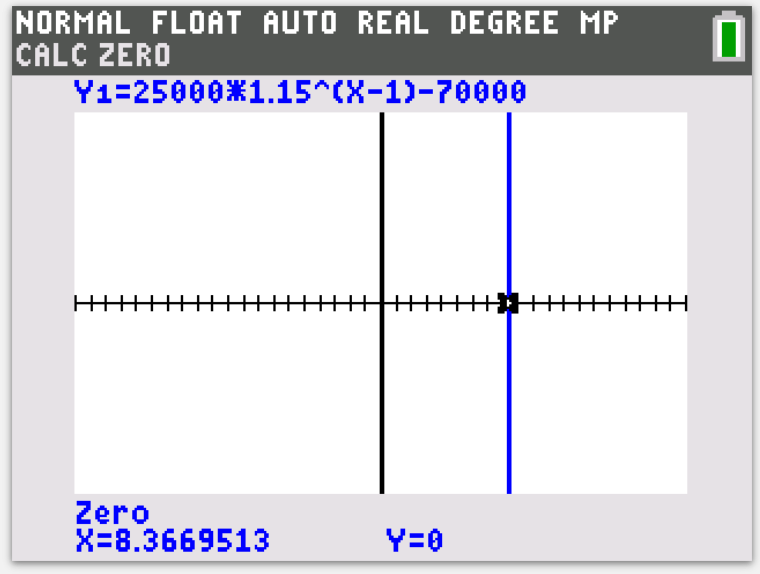
A population of birds on an island starts at 25000 at the end of 2015 and it is expected to grow by 15% each year.
a) Find the general formula of this sequence.
b) Find the expected population size after 4 years, rounded to 2 decimal points.
c) Find the number of full years it will take it to reach 70000.
Answers and Explanations
Show Answer
a) 38021.88
b) \(u_n = 25000 * 1.15^{n-1}\)
c) 9
Question 6
Calculator
[Maximum mark: 5]
A dad took his daughter to a playing ground. They start playing on a swing, where the first swing was 3m long and every next swing was 90% of the previous one. Her dad gives her a push when the length of the swing falls below 0.5m.
a) Find the length of the fourth swing
b) How many swings will it take for the dad to need to give a push?
Question 7
Calculator
[Maximum mark: 8]
Jake has a car shop in which he sells two car brands: Brand A and Brand B. Brand A costs more, $30,000, and its depreciation is 15% per year. Cars of Brand B cost $25,000.
Mike bought one of the cars from Brand B, and turns out that after two years it is worth $20,250.
a) Calculate the depraciation rate of Brand B.
b) What will be the value of a car from Brand A after 5 years? (round to 2 decimals)
c) Find how many years will it take for the car from Brand B to be worth more than the car from Brand A. Round your answer to two decimals
Question 8
No Calculator
[Maximum mark: 10]
Let \(u_n = 4n + 3\), for \(n \in \mathbb{Z}^+\)
a) Is this series geometric or arithmetic?
b) Hence, find the common difference.
c) Represent the sum of the first 5 terms using sigma notation.
d) Find the sum of the first 10 terms of this series.
Answers and Explanations
Show Answer
a) Arithmetic
b) 4
c) \(\sum_{n=1}^{5} (4n + 3)\)
d) 250
Question 9
Calculator
[Maximum mark: 12]
Consider a sequence in which its respective terms are:
\[u_2 = 250, \ u_3 = 275, \ u_4 = 300\]
You may assume that the sequence continues in the same pattern.
a) Find the value of \( u_{25} \).
b) Find the sum of the first 15 terms of this sequence.
c) Find the first term of the sequence which crosses the value of 1000.
Now, consider another sequence:
\[w_3 = 9, \ w_4 = 27, \ w_5 = 81\]
d) Find \( u_{1} \).
e) Represent the sum of the first 4 terms of this sequence with the sigma notation.
f) Find the first term at which the second sequence will have a greater value than the first sequence.
Answers and Explanations
Show Answer
a) 825
b) 6000
c) 33
d) 1
e) \(\sum_{n=1}^{4} (3^{n-1})\)
f) 7
Question 10
Calculator
[Maximum mark: 8]
Lisa invests $12,000 into a savings account that pays an annual interest rate of 4.75%, compounded annually.
Round your answers to two decimal points.
a) Write down a formula which calculates the total value of the investment after “n” years.
b) Calculate the amount of money in the savings account after:
i. 2 years
ii. 5 years
iii. 10 years
c) Lisa wants to use this money to put down a $15,000 deposit on her car. Determine if she will be able to do this within a 5-year timeframe.
Answers and Explanations
Show Answer
a) \(12000 * 1.0475^n\)
b) (i) $13167.08
b) (ii) $15133.92
b) (iii) $19086.29
c) Yes
Question 11
Calculator
[Maximum mark: 8]
Emma buys a car for $32,500. The value of the car depreciates by 10% each year.
Round your answers to two decimal points.
a) Find the value of the car after 8 years.
Alex buys a car for $18,000. The car depreciates by a fixed amount each year, and after 5 years, it is worth $9,200.
b) Determine the annual rate of depreciation for Alex's car.
Question 12
No Calculator
[Maximum mark: 7]
An arithmetic sequence is given, with u1 = 1.2 and u5 = 0.4.
a) Find \( d \).
b) Find the expression \( u_{n} \).
The table below shows a probability distribution of a random discrete variable \( X \), where \(P(X=n) = \frac{u_n}{k+1}\) where \(n \in \mathbb{Z}^+, 1 \leq n \leq 5 \text{ and } k \in \mathbb{R}^+\)
| n |
1 |
2 |
3 |
4 |
5 |
| \(P(X=n)\) |
\(\frac{1.2}{k+1}\) |
\(\frac{u_2}{k+1}\) |
\(\frac{u_3}{k+1}\) |
\(\frac{u_4}{k+1}\) |
\(\frac{0.4}{k+1}\) |
b) Find \( k \).
Question 13
Calculator
[Maximum mark: 7]
John bought a Honda motorcycle for $20,000 which depreciates by 4% each year.
a) Find the total amount the motorcycle will depreciate after 6 years (round your answer to two decimal points).
The value of a Suzuki motorcycle that John was considering which costs $25,000 but its value depreciates by 9% each year.
b) What will be the difference in the values of Honda and Suzuki motorcycles after 3 years? (round your answer to two decimal points)
c) After how many full years will the value of Honda motorcycle be higher than that of Suzuki?
Question 14
Calculator
[Maximum mark: 6]
Mark currently has $10,000 which he wants to double his money quickly. The first option is safer, meaning he puts money into a savings account, which has an annual interest rate of 5.5% compounded quarterly.
a) How many years will it take Mark to double his money with this method? Round your answer to two decimals.
He thinks the time taken for doubling with the first method is too long, so he finds another one – investing in a high-growth stock with large risk associated to it. He thinks he will be able to double his money in 6 years with that option.
b) What interest rate (compounded yearly) does this option need to have for him to double his money in 4 years? Round your answer to two decimals.
Question 15
No Calculator
[Maximum mark: 6]
Consider an arithmetic sequence \(u_1, u_2, u_3, u_4,...\)
The sum of the first \(n\) terms of this sequence is given by \(S_n = 2n^2 -n\).
a) Find the sum of the first 4 terms.
b) Given that the sum of the first 5 terms is 45, find:
i. \(u_5\)
ii. \(u_1\)
iii. \(u_n\)
Consider a gemoetric sequence \(w_n\) where \(w_1 = u_1\) and \(w_3 = u_3\).
c) Find the possible values of \( r \).
d) Given that \(v_6 > 0\), select one possible value of \( r \).
Answers and Explanations
Show Answer
a) 28
b) (i) 17
b) (ii) 1
b) (iii) 4n - 3
c) r = 3, r = -3
c) r = 3
Question 16
Calculator
[Maximum mark: 6]
Sam invests $40,000 into an investment fund which pays a nominal annual interest rate of 5.5% compounded monthly.
Round your answers to two decimal points.
a) Calculate the money in his investment fund after 5 years.
b) How many years will it take for the money to reach $60,000?
Question 17
Calculator
[Maximum mark: 6]
In 2010, Sam put $12,000 into his savings account with a 5% interest rate p.a. compounded quarterly.
Round your answers to two decimal points.
a) How much money will be in his bank account after 3 years?
b) Without calculating, do you think the value will be higher or lower if the interest was compounded yearly?
c) Calculate the value after 3 years with yearly compounding.
Question 18
Calculator
[Maximum mark: 6]
Tony buys a BMW for $35,000. It is known that the value of the car depreciates by 8% every year.
Round your answers to two decimal points.
a) Find the difference between the starting car value and the car value after it has depreciated for 5 years. Round your answer to two decimal points.
The value of a Mercedes depreciates by 5% every year.
b) What would have to be the value of this Mercedes such that the value of BMW is equal to the value of Mercedes after 6 years of both cars depreciating? Round your answer to two decimal points.