Question 1
[Maximum mark: 2]
State the purpose of the memory address register (MAR).
Question 2
[Maximum mark: 3]
Assume \(P = 3\) and \(Q = 6\).
Determine the value of the following expression: \[(P \geq Q) \text{ NOR } (P \leq 5)\]
Question 3
[Maximum mark: 4]
Answer the following questions:
(a) Identify one characteristic of random access memory (RAM).
(b) Explain the use of cache memory.
Question 4
[Maximum mark: 4]
Construct a truth table for the logic expression: A NAND (B NOR C).
Question 5
[Maximum mark: 2]
Explain how cache memory affects system performance.
Question 6
[Maximum mark: 4]
Calculate and show your workings:
a) the binary (base 2) value of the denary (base 10) number: 105
b) the hexadecimal (base 16) value of the denary (base 10) number: 200
Question 7
[Maximum mark: 4]
Construct a truth table for the logic expression: (X XOR Y) AND Z.
Question 8
[Maximum mark: 6]
Draw a truth table for the following logic circuit:
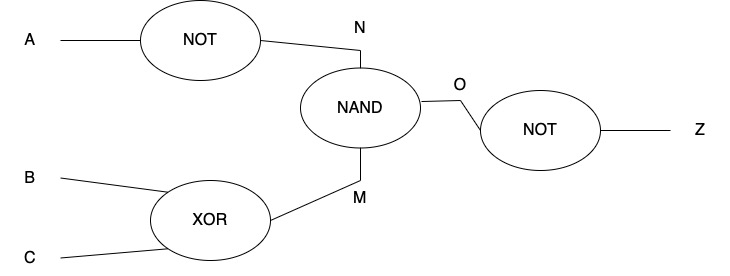
Question 9
[Maximum mark: 2]
Outline the need for a translation process from high level language to machine code.
Question 10
[Maximum mark: 2]
Outline two functions of a web browser.
Question 11
[Maximum mark: 5]
Assume \(X = 7\) and \(Y = 3\).
Determine the value of the following expression: \[(X \leq 6) \text{ XOR } (Y > X)\]
Question 12
[Maximum mark: 2]
Explain why compression of data is beneficial when transmitting data files across a network.
Question 13
[Maximum mark: 5]
Assume \(A = 3\), \(B = 5\), and \(C = 11\)
Determine the value of the following expression: \[((A \leq B) \text{ XOR } (C > B)) \text{ AND } (A \text{ < } B)\]
Question 14
[Maximum mark: 2]
Outline one reason why computers use the binary number system.
Question 15
[Maximum mark: 2]
Outline two differences between primary and secondary storage.
Question 16
[Maximum mark: 2]
Outline the reason for compression when transmitting data.
Question 17
[Maximum mark: 2]
Describe the function of the control unit (CU).
Question 18
[Maximum mark: 1]
Give one reason why the cache memory can speed up the functioning of a processor.
Question 19
[Maximum mark: 2]
State the binary representation of the hexadecimal number 3C.
Question 20
[Maximum mark: 4]
Construct a truth table for the Boolean expression NOT (A OR B) NAND C. Use the headings given below.
| A |
B |
C |
A OR B |
NOT (A OR B) |
NOT (A OR B) NAND C |
|
|
|
|
|
|
Question 21
[Maximum mark: 3]
Describe how memory management is used to prevent the system from crashing.
Question 22
[Maximum mark: 3]
Explain how the use of media access control (MAC) addresses can improve security.
Question 23
[Maximum mark: 2]
Calculate how many different colours can be represented using two hexadecimal characters.
Question 24
[Maximum mark: 8]
a) Outline the differences between random access memory (RAM) and read only memory (ROM).
b) Describe how the operating system manages the primary memory.
c) Explain the roles of the data bus and address bus.
Question 25
[Maximum mark: 1]
State the part of the central processing unit (CPU) which is responsible for performing
calculations.
Question 26
[Maximum mark: 2]
State the hexadecimal equivalent of the following binary number: 100111001.
Question 27
[Maximum mark: 4]
Colours are represented by a computer as a combination of the three primary colours: red, green and blue.
Numerical values are used to represent the different shades of each primary colour. These values range from 0 to 255 in decimal and 00 to FF in hexadecimal.
a) State the number of bits used to represent a non-primary colour, like purple.
b) State the maximum number of colours that can be represented in a computer pixel.
Question 28
[Maximum mark: 4]
Complete the following truth table where:
\[ X = A \ \text{NOR} \ B \]
\[ Y = A \ \text{AND} \ C \]
\[ Z = X \ \text{XOR} \ Y \]
